Raymond Smullyan defines the following types of reasoners:
- Accurate reasoner: An accurate reasoner never believes any false proposition. (modal axiom T)

- Inaccurate reasoner: An inaccurate reasoner believes at least one false proposition.

- Conceited reasoner:
A conceited reasoner believes his or her beliefs are never inaccurate. A
conceited reasoner will necessarily lapse into an inaccuracy.
![\mathcal{B}[\neg\exists p: \neg p \wedge \mathcal{B}p]](http://upload.wikimedia.org/math/7/3/1/731323b651a930db5b5c526ea8a62342.png)
- or
![\mathcal{B}[\forall p: \mathcal{B}p \to p]](http://upload.wikimedia.org/math/2/8/1/2818682c12672bd799b2ed7c67a391d5.png)
- Consistent reasoner: A consistent reasoner never simultaneously believes a proposition and its negation. (modal axiom D)

- or

- Normal reasoner: A normal reasoner is one who, while believing p, also believes he or she believes p (modal axiom 4).

- Peculiar reasoner:
A peculiar reasoner believes proposition p while also believing he or
she does not believe p. Although a peculiar reasoner may seem like a
strange psychological phenomenon (see Moore's paradox), a peculiar reasoner is necessarily inaccurate but not necessarily inconsistent.

- Regular reasoner: A regular reasoner is one who, while believing
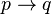 , also believes
, also believes  .
.

- Reflexive reasoner:] A reflexive reasoner is one for whom every proposition p has some q such that the reasoner believes
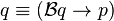 .
.

- If a reflexive reasoner of type 4 believes
 , he or she will believe p. This is a parallelism of Löb's theorem for reasoners.
, he or she will believe p. This is a parallelism of Löb's theorem for reasoners.
- Unstable reasoner:
An unstable reasoner is one who believes that he or she believes some
proposition, but in fact does not believe it. This is just as strange a
psychological phenomenon as peculiarity; however, an unstable reasoner
is not necessarily inconsistent.

- Stable reasoner:
A stable reasoner is not unstable. That is, for every p, if he or she
believes Bp then he or she believes p. Note that stability is the
converse of normality. We will say that a reasoner believes he or she is
stable if for every proposition p, he or she believes BBp→Bp
(believing: "If I should ever believe that I believe p, then I really
will believe p").

- Modest reasoner: A modest reasoner is one for whom every believed proposition p,
 only if he or she believes p. A modest reasoner never believes Bp→p
unless he or she believes p. Any reflexive reasoner of type 4 is modest.
(Löb's Theorem)
only if he or she believes p. A modest reasoner never believes Bp→p
unless he or she believes p. Any reflexive reasoner of type 4 is modest.
(Löb's Theorem)

- Queer reasoner: A queer reasoner is of type G and believes he or she is inconsistent—but is wrong in this belief.
- Timid reasoner: A timid reasoner is afraid to believe p [i.e., he or she does not believe p] if he or she believes

![\mathcal{B}[\neg\exists p: \neg p \wedge \mathcal{B}p]](http://upload.wikimedia.org/math/7/3/1/731323b651a930db5b5c526ea8a62342.png)
![\mathcal{B}[\forall p: \mathcal{B}p \to p]](http://upload.wikimedia.org/math/2/8/1/2818682c12672bd799b2ed7c67a391d5.png)


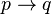 , also believes
, also believes  .
.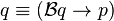 .
. , he or she will believe p. This is a parallelism of Löb's theorem for reasoners.
, he or she will believe p. This is a parallelism of Löb's theorem for reasoners. only if he or she believes p. A modest reasoner never believes Bp→p
unless he or she believes p. Any reflexive reasoner of type 4 is modest.
(Löb's Theorem)
only if he or she believes p. A modest reasoner never believes Bp→p
unless he or she believes p. Any reflexive reasoner of type 4 is modest.
(Löb's Theorem)









1 comment:
So a queer reasoner disbelieves in the consistency of own their own reasoning? That applies to a lot of people, and from a variety of convictions too...
Post a Comment